Web-based interactive learning package

Introduction of Group Velocity and Energy Flux
Group Velocity
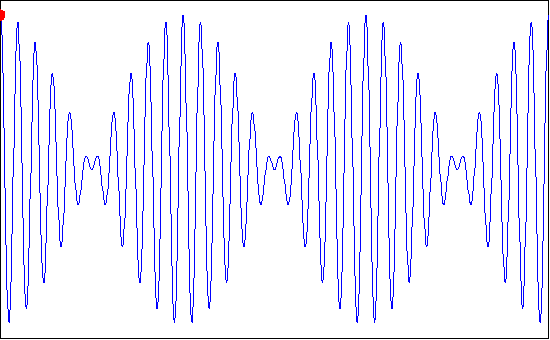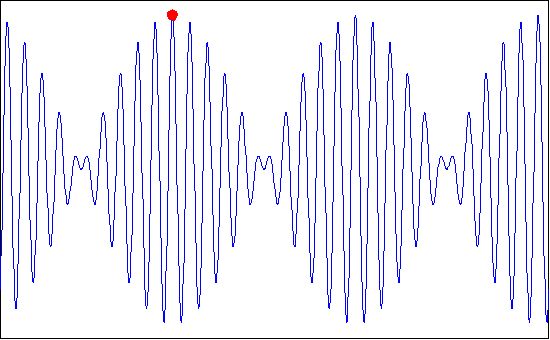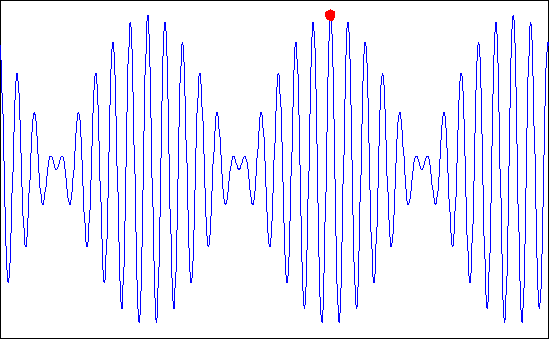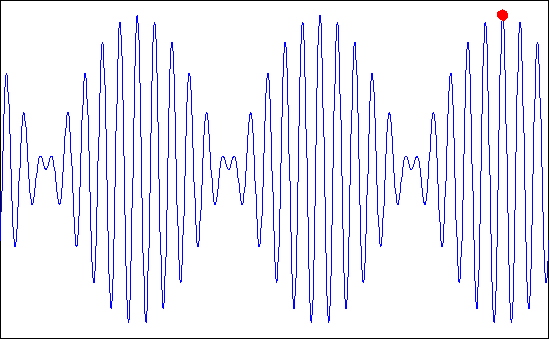
The group velocity in terms of the rate at which energy is being transferred by a train of propagating waves can be derived. On the other hand, a more descriptive explanation of the term group velocity results from examining the propagation of a group of waves.
If there are two trains of waves of the same height propagating in the same direction with slightly different frequencies and wave numbers, they are superimposed as
ƞ = ƞl + ƞ2
ƞ = H/2 cos (k1x1- ơ1t1) + H/2 cos (k2x2 - ơ2t2)
where
ơ1 = ơ - ∆ơ/2, k1 = k - ∆k/2
ơ2 = ơ + ∆ơ/2, k2 = k + ∆k/2
Using trigonometric identities, the profiles can be combined in the following manner:
ƞ = Hcos {1/2 [(k1+k2)x + (ơ1 + ơ2)t]} cos{1/2[(k1 - k2)x-(ơ1-ơ2)t]}
=H cos(kx - ơ t)cos[1/2/ ∆k (x-(∆ơ/∆k)t)]
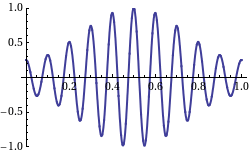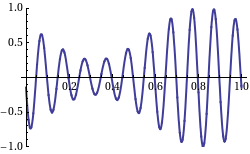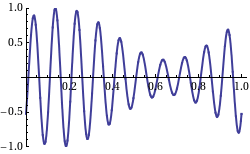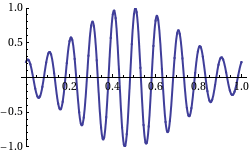
The resulting profile, consisting of wave forms moving with velocity C = ơ/k,is modulated by an “envelope” that propagates with speed ∆ơ/∆k, which is referred to as the group velocity Cg. The superimposed profile is shown in figure as below.
If we recall that the wave energy is proportional to the wave height, it is clear that no energy can propagate past a node as the wave height (and therefore dynamic pressure) is zero there. Therefore, the energy must travel with the speed of the group of waves. This velocity is seen to be, from the above equation,
Cg = ∆ơ/∆k

Energy Flux
Small-amplitude water waves do not transmit mass as they propagate across a fluid, as the trajectories of the water particles are closed. However, water waves do transmit energy. For example, consider the waves generated by a stone impacting on an initially quiescent water surface.A portion of the kinetic energy of the stone is transformed into wave energy. As these waves travel to and perhaps break on the shoreline, it is clear that there has been a transfer of energy away from the generation area. The rate at which the energy is transferred is called the energy flux 𝓕, and for linear theory it is the rate at which work is being done by the fluid on one side of a vertical section on the fluid on the other side. For the vertical section AA’,shown in Figure 4.10, the instantaneous rate at which work is being done by the dynamic pressure [ pᴰ= (p +pgz)] per unit width in the direction of wave propagation is
𝓕 = ∫ pD﹒u dz ,to integrate it from -h to ƞ
The average energy flux is obtained as before by averaging over a wave period
Ḟ = 1/T ∫ ∫ pD﹒u dz dt
By using the dispersion relationship, the equation can be rearranged into the following:
Ḟ = (1/8 𝜌gH² ) ơ/k [ 1/2 ( 1 + 2kh/sinh(2kh) ) ]
Ḟ = ECn
where Cn is the speed at which the energy is transmitted; this velocity is called the group velocity Cg
and E = 1/8 𝜌gH² , C = ơ/k, n = 1/2 ( 1 + 2kh/sinh(2kh) )