Web-based interactive learning package
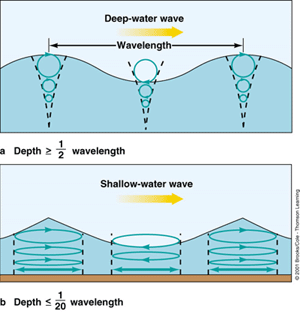
The solutions developed for standing and progressive small- amplitude water waves provide the basis for applications to numerous problems of engineering interest. For example, the water particle kinematics and the pressure field within the waves are directly related to the calculation of forces on bodies. The transformation of waves as they propagate toward shore is also important, as in many cases coastal engineeringdesign involves the forecasting of offshore wave climates or the use of offshore data, for example, those obtained from ships. It is obviously necessary to be able to determine any modifications that occur to these waves as they encounter shallower water and approach the shore.

Engineering Properties
Engineering Wave Properties includes:
-
Wave Particles Displacement
-
Wave Particles Velocity & Acceleration
-
Velocity Potential and Stream Function
Wave Particles Displacement
The trajectory of the water particle depends on the few parameters of the water wave such as wavelength, water depth, celerity, wave period and the elevation of the particle. The sharp of the trajectory of the particles will changed based on those parameters as well. The relationship between the trajectory of the particles and the parameters of the water wave is described as following equations.
The relationships between the trajectory of the particles and the parameters of the water wave also can be demonstrated by interactive animation created. The parameters of the water wave can be changed by dragging and sliding the bar which represent each parameter of the water wave. Once the parameter was changed, the trajectory will update simultaneously. Just click on the link to the page of the interactive animation to experience on it.
http://web.mit.edu/~njwilson/www/waves.html
Wave Particles Velocity & Acceleration
Examining the horizontal and vertical velocity components as a function of position, it is clear that they are 90" out of phase; the extreme values of the horizontal velocity appear at the phase positions (kx - ơt) = 0, 𝜋,... (under the crest and trough positions), while the extreme vertical velocities appear at 𝜋/2, 3𝜋/2, …(where the water surface displacement is zero).
The vertical variation of the velocity components is best viewed by starting at the bottom where k( h + z ) = 0. Here the hyperbolic terms involving z in both the u and w velocities are at their minima, 1 and 0, respectively. As we progress upward in the fluid, the magnitudes of the velocity components increase. In Figure 4.1, the velocity components are plotted for four phase positions. The accelerations are such that the maximum vertical accelerations occur as the horizontal velocities are extremes and the same is true for the vertical velocities and the horizontal accelerations.

Velocity Potential and Stream Function
For convenience, the velocity potential has been used to develop the small-amplitude wave theory, yet often it is convenient to use the stream function representation. Therefore, we can use the Cauchy-Riemann equations to develop them from the velocity potentials.
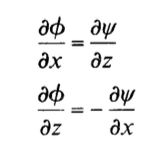
Progressive Wave

Standing Waves
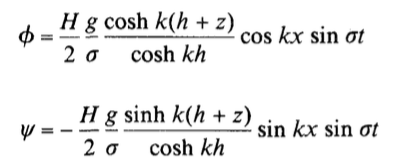
The streamlines and velocity potential for both cases are shown in Figure as follow. The streamlines and potential lines are lines of constant Ѱ and 𝜙 respectively.
